Graphs in Data Structure are one of the most important and widely used in computer science. We use them to represent connections or relationships between objects, which makes them useful in many real-life applications
Graphs in Data Structure
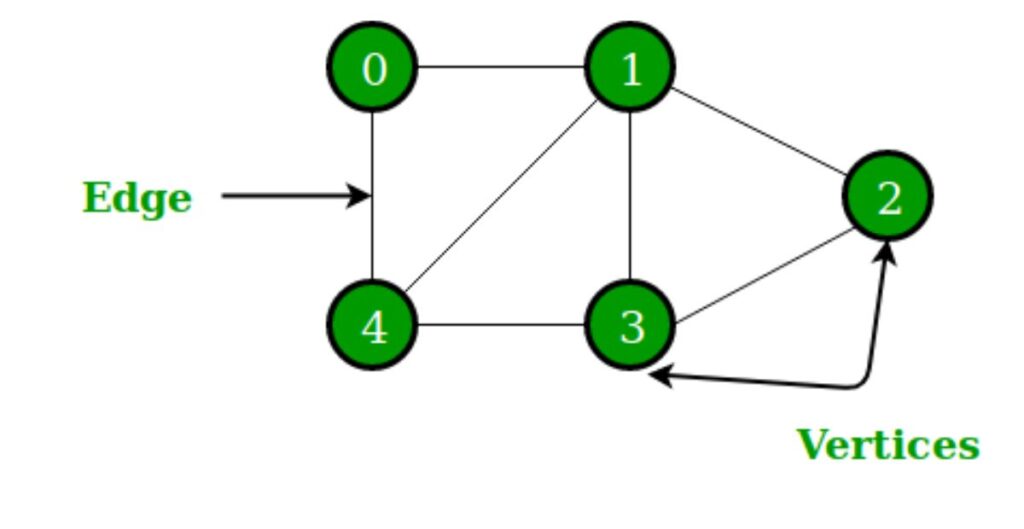
A graphs data structure is a non linear data structure which is having a connection between objects using vertices (also called nodes) and edges. Edges connect pairs of vertices, and we use this structure to model the relationships between those objects.
Here’s the more in detailed breakdown:
Vertices (Nodes):
The individual objects or points within the graph which represents entities like cities on the map, users in the social media, or computers in the network
Edges:
The connections between the vertices that represents the relationships or interaction s between the objects. For example an edge can represent a road connecting two cities, a friendship between 2 people, or a communication between 2 people
Want to learn about types of Queue
Types of Graphs
1. Finite Graphs:
A finite graph is a type of graphs in data structure which has a finite (countable) number of vertices and edges, i.e. If a graph G=(V,E) consists of a finite number of vertices and edges denoted by V and E respectively, then the graph is a finite graph.
2. Infinite Graph:
An infinite graph is a type of graph in data structure which has infinite number of vertices and edges, i.e. If a graph G=(V,E) consists of an uncountable number of vertices or edges denoted by V and E respectively, then the graph is an infinite graph.
3. Trivial Graph:
We call a graph a trivial graph if it has only one vertex.
4. Simple Graph:
A simple graph is a graph that does not contain more than one edge between the pair of vertices. A simple railway track connecting different cities is an example of a simple graph.
5. Multi Graph:
We call a graph a multigraph if it contains some parallel edges but doesn’t contain any self-loop. For example a Road Map.
6. Null Graph:
We call a graph of order n and size zero a graph where only isolated vertices exist with no edges connecting any pair of vertices. We call such a graph a null graph if it has no edges at all. In other words, it is a graph with only vertices and no connections between them. We can also refer to a null graph as an edgeless graph, an isolated graph, or a discrete graph.
7. Complete Graph:
A simple graph with n vertices becomes a complete graph when each vertex has a degree of n-1, meaning it connects to the other n-1 vertices. We also call a complete graph a full graph.
8.Directed Graphs:
A graph in which edges have a direction, i.e., the edges have arrows indicating the direction of traversal.
9. Undirected Graphs:
If the graph connects both ways, you can travel in either direction between two connected places.
10. Weighted Graphs:
A weighted graph is a graph where each edge has a number (weight) that represents distance, cost, or time. These graphs help find the shortest or cheapest paths. Examples include Google Maps, airline routes, and delivery networks.
11. Unweighted Graphs:
An unweighted graph treats all edges equally, without assigning any values like distance or cost. It simply shows connections between points. Examples include basic social networks and metro maps without travel times.
12. Pseudo Graph:
We call a graph G a pseudograph if it has a self-loop and some multiple edges. A pseudograph is a type of graph that allows for the existence of self-loops (edges that connect a vertex to itself) and multiple edges (more than one edge connecting two vertices). In contrast, a simple graph is a graph that does not allow for loops or multiple edges.
13. Regular Graph:
We call a simple graph regular if all vertices in graph G have the same degree. All complete graphs are regular but vice versa is not possible. A regular graph is a type of undirected graph where every vertex has the same number of edges or neighbors. In other words, if a graph is regular, then every vertex has the same degree.
14. Bipatite Graph:
We call a graph bipartite if we can divide its vertices into two disjoint sets such that every edge connects a vertex from one set to a vertex in the other set.
15. Labeled Graph:
A graph becomes a labeled graph when we label its vertices and edges with names, dates, or weights. We also call it a weighted graph.
16. Sparse Graphs:
A graph with relatively few edges compared to the number of vertices. Example: A chemical reaction graph where each vertex represents a chemical compound and each edge represents a reaction between two compounds.
17. Dense Graphs:
A graph with many edges compared to the number of vertices. Example: A social network graph where each vertex represents a person and each edge represents a friendship.
18. Digraph Graph:
We call a graph G = (V, E) a digraph if it has a mapping f such that every edge maps onto an ordered pair of vertices (Vi, Vj). We also call it a directed graph. The ordered pair (Vi, Vj) means an edge between Vi and Vj with an arrow directed from Vi to Vj. Here in the figure: e1 = (V1, V2) e2 = (V2, V3) e4 = (V2, V4)
19. Subgraph:
We call a graph G1 = (V1, E1) a subgraph of graph G(V, E) if V1 is a subset of V and E1 is a subset of E, such that each edge in G1 has the same end vertices as in.
20. Connected or Disconnected Graph:
We call a graph G connected if any pair of vertices (Vi, Vj) is reachable from one another. In other words, we call a graph connected if we can find at least one path between every pair of vertices in G. If no such path exists for some pairs, we call the graph disconnected. A null graph with n vertices is a disconnected graph consisting of n components. Each component consists of one vertex and no edge.
21. Cyclic Graph:
We call a graph G a cyclic graph if it consists of n vertices (where n ≥ 3), labeled as V1, V2, V3, …, Vn, and edges like (V1, V2), (V2, V3), (V3, V4), …, (Vn, V1) that form a closed loop.
22. Trees:
A connected graph with no cycles. For example, we can represent a family tree where each person connects to their parents.
Graph Representation
1. Adjacency Matrix:
Let’s assume there are n vertices in the graph So, create a 2D matrix adjMat[n][n] having dimension n x n.
- If there is an edge from vertex i to j, mark adjMat[i][j] as 1.
- If there is no edge from vertex i to j, mark adjMat[i][j] as 0.
2. Adjacency List:
We use an array of lists to store edges between two vertices. The size of array is equal to the number of vertices (i.e, n). Each index in this array represents a specific vertex in the graph. The entry at the index i of the array contains a linked list containing the vertices that are adjacent to vertex i. Let’s assume there are n vertices in the graph So, create an array of list of size n as adjList[n].
- “Vertex 0 connects to all the nodes stored in adjList[0].
- Similarly, vertex 1 connects to all the nodes stored in adjList[1], and so on.
Basic Operations on Graphs
- Add Vertex – Insert a node.
- Add Edge – Connect two nodes.
- Remove Vertex – Delete a node and its edges.
- Remove Edge – Delete a connection.
- Search/Traversal – Visit nodes using DFS or BFS.
Graph Traversal Techniques
1. BFS Graph Traversal:
Breadth-First Search (BFS) is a graph traversal algorithm, where we start from a selected(source) node and traverse the graph level by level, by exploring the neighbor nodes at each level.
2. DFS Graph Traversal:
Depth First Search (DFS) is a graph traversal algorithm where we start from a selected (source) node and recursively visit its children, going deeper into the graph until we reach a node with no unvisited children. When we reach a dead-end, the algorithm backtracks and visits the other children of the previous nodes.
Applications of Graph
- Navigation Systems – Google Maps, Uber.
- Social Networks – Facebook, LinkedIn.
- Web Crawling – Search engines crawling websites.
- Network Routing – Internet data transfer.
- Recommendation Engines – Netflix, Amazon suggestions.
- Dependency Management – Software package installations.
Conclusion
Graphs are everywhere — from your favorite social media apps to navigation tools. Understanding graphs helps solve complex problems related to networks, paths, and relationships in real-world systems.
FAQ:
Applications of graph
Types of graphs
Trees and graphs in data structure
Directed graph
Breadth-First Search (BFS)
Depth First Search (DFS)
Applications of graph
Operations of graph
f6a1zl